
The safety of cataract surgery has reached the point at which it is safer to undergo extraction by a competent surgeon than to live life with a cataract. This means that patients more commonly judge the success of their surgery not by how well they can see but by how well they can see without glasses. We surgeons must never forget that the primary purpose of cataract surgery is to prevent the inevitable decline into blindness; nevertheless, cataract surgery gives us an opportunity to grant patients the wonderful freedom of life without glasses. This starts with biometry.

It’s All in the Numbers
The IOL calculation formula is simple arithmetic. If we put in the correct numbers, we will always get the correct IOL power, and the patient will achieve the desired postoperative refraction. The reason so many patients do not achieve emmetropia is that usually some or all of the numbers we use are incorrect. In contemporary biometry, we measure some parameters and guess others, and many of the assumptions we make will be wrong for a given patient.

But We Must Make Assumptions
The one parameter we can measure accurately is axial length. In fact, we can measure axial length more accurately than is required for precise IOL calculations. It is in the estimation of corneal power that we are forced to make assumptions, and these assumptions frequently lead to erroneous corneal power readings being used in IOL formulas. The cornea provides 66% of the refractive power of the eye, so even a 2% error can lead to a miscalculation of 1.00 D.
AT A GLANCE
• The reason many patients do not achieve emmetropia is that usually some or all of the numbers used in IOL calculations are incorrect.
• Current biometry technology forces surgeons to make guesses about data they cannot measure accurately in each individual patient.
• No further improvement in biometry is possible with current methods; only a breakthrough in new technology will deliver this paradigm shift.
In addition, when we enter data into any formula, an assumption is made about where the IOL will sit in the eye; this is the calculation of effective lens position (ELP). Different formulas use different methods to do this, but, in all formulas, the ELP is only a prediction. The effect of the ELP can be summarized by this rule of thumb: A 1-mm shift in the anteroposterior position of the IOL causes a 10% shift of power. That is to say, an eye with a 23.00 D IOL sitting 0.5 mm further forward than the predicted ELP will be almost 1.20 D myopic.
The rest of this article explores the processes of biometry to elucidate what we can measure, what we must assume, and what we must guess.

Measuring Corneal Power (With Assumptions)
It is common practice to record the corneal power or keratometry (K) readings first, before performing any other tests that might affect corneal curvature such as applanation tonometry. The principle of physics that measures corneal power is the same in all keratometers. The size of an image reflected from the surface of the cornea is a measure of its curvature. A flatter curve will produce a larger image, and a steeper curve will produce a smaller image. All keratometers measure the image size and convert that size to a curvature.
With a Javal-Schiotz–style keratometer, two mires are shone onto the cornea and an observer adjusts their position until they are separated by a fixed distance. The observer then reads the scale, which is calibrated in either diopters or millimeters. In a fixed image–sized keratometer such as the KM-500 (Nidek) or IOLMaster (Carl Zeiss Meditec), a circle of lights is shone onto the cornea and a video image is taken. The distances of each spot of light from the center are measured, and, in this way, the curvature is calculated. The software can give the reading in either diopters or millimeters. Already, readers may be starting to feel slightly concerned about the accuracy of such a method to measure the refractive power of the cornea.
This concern should increase when we look at how such a method is also highly technique-dependent as well as reliant on whether the keratometer has been calibrated. An out-of-focus eyepiece or an uncorrected refractive error in the observer can cause an error of up to 1.00 D. The calibration of all such devices is done using a spherical surface, but the cornea is aspheric. If the patient is not fixated properly on the target, the wrong area of the cornea will be measured. How many surgeons know how to calibrate their keratometer (or even check its calibration), correctly adjust the eyepiece for their own refractive error, and correctly align the patient’s eye for an optimal measurement? Even automated keratometry, such as that in the Lenstar (Haag-Streit) or IOLMaster, is dependent on technique to get reliable measurements. After all this, we are, in fact, only measuring the curvature of the front surface on the tear film, and we expect this to reliably give us the full refracting power of the cornea.
But the guessing does not stop there. That curvature is then converted to a dioptric power using the formula D = (i-1)/r, where i is the refractive index of the cornea and r is the radius of curvature in meters. This formula is an approximation, and it ignores the curvature on the back of the cornea because it is not measurable and has a minimal effect. Even in patients who might have an astigmatic posterior surface, the same limitations apply.
We assume that the refractive index of the corneal tissue is 1.3375 for all humans. It is, however, highly likely that there is wide variation in the refractive index of the human cornea, both in its virgin state and after refractive surgery. Because we cannot measure the refractive index in any individual patient, we are forced to make a guess.
By this stage, we have assumed that the spherical calibration ball we used to calibrate the keratometer will measure the curvature of the aspheric tear film on the front of the cornea and have guessed that the refractive index of the corneal tissue is 1.3375 and that the contour of the back of the cornea is within an average range. All of this guessing is used just to attempt to measure the refracting power of the element that gives the eye 66% of its light-bending property.
It is now clear that we get the corneal power right only when our assumptions are correct for a particular eye, or when an error in one assumption is cancelled by an opposite error in another. Probability states that we get close to the correct answer most of the time, but, when errors sum rather than cancel, the patient can be left with significant postoperative refractive error.

Measuring Axial Length
The axial length of the eye is possibly the easiest measurement to perform and an area where error causes the least refractive disappointment postoperatively. All measurement techniques depend on sending a wave of energy through the cornea to the retina and timing its return. Knowing the speed of the waveform and the time it takes to return allows the distance to be calculated: distance = time x speed. Already, we can see that some approximations are made in this calculation, most notably the speed of the waveform through the eye. Looking at how ultrasound measures axial length is the easiest way to understand the challenge.
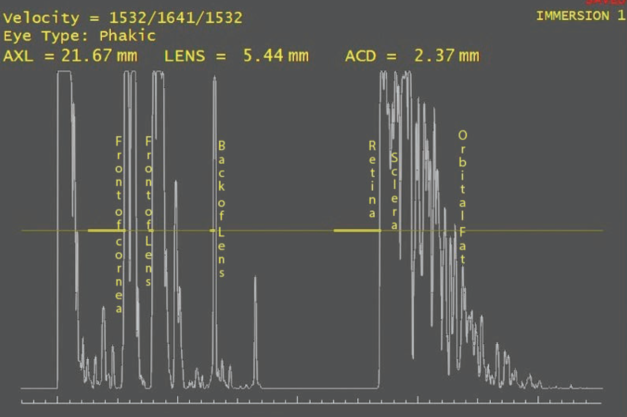
Figure 1. Typical immersion scan of an eye showing the acoustic interfaces.
Ten million times a second, a sound wave leaves the piezoelectric crystal in the tip of the ultrasound probe. To a sound wave, the eye is a series of acoustic interfaces (Figure 1). An acoustic interface is simply the junction of two media with two differing sound propagation properties. A sound wave transiting an acoustic interface gives rise to an echo: that is, some of the energy bounces back off the interface. The angle of reflection of the sound wave is determined by the angle of incidence, as is the case with light. If the angle of incidence is perpendicular, then the sound will travel back exactly along the path it came on.
Eventually, the sound wave will arrive back at the probe and excite the piezoelectric crystal, giving rise to a signal that is detected by the device’s software. The software knows what time the sound wave left and what time it returned, so all we have to do is tell it the speed at which the sound wave was traveling so that it can work out the distance traveled.
In immersion ultrasound, the first acoustic interfaces are the front and back of the cornea. The software marks this echo as the front of the eye. The sound wave then traverses the anterior chamber to reach the next acoustic interface, which is the front of the lens. The speed of sound in the aqueous is 1,550 m/sec. The echo from the aqueous-lens interface returns to the ultrasound probe and stimulates the piezoelectric crystal, generating an electric current. The timing of this current together with the known sound velocity in aqueous allows the calculation of the distance of the cornea to the front of the lens, the preoperative anterior chamber depth (ACD).
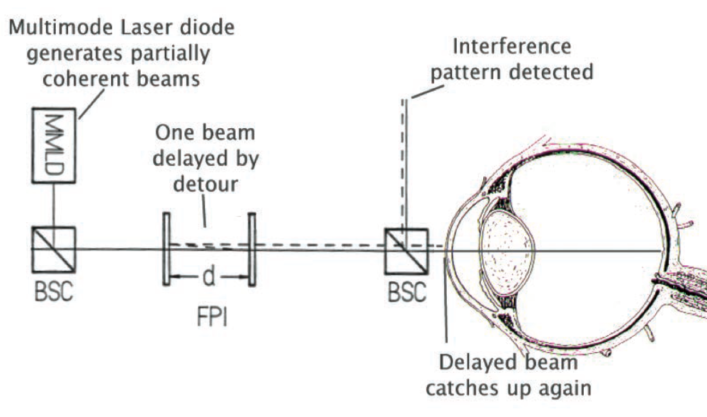
Figure 2. In optical biometry, the distance between two mirrors is adjusted to restore the interference pattern at the detector. The inter-mirror distance is then used as a measure for the length of the eye.
The next interface is the back of the lens, although frequently the front and back of a sclerotic nucleus can be clearly detected. The sound speed used for the lens in every ultrasound machine is 1,660 m/sec, despite research showing that the average sound speed through a cataractous lens is about 1,646 m/sec. As before, when the echo from the back of the lens returns to the probe, the same calculation is made and the lens thickness is measured. Finally, the echo from the internal limiting membrane returns to the probe, and, assuming a sound speed of 1,550 m/sec in the vitreous, the distance from the back of the lens to the fovea can be calculated. The axial length is the sum of these three distances (preoperative ACD + lens thickness + vitreous distance = axial length).
Similar principles of physics apply in optical biometry. In 1887, Albert A. Michelson and Edward W. Morley used interferometry to measure the difference in path distance on two light beams. Today, using partial coherence interferometry, the same physical principle is used to estimate the axial length of the eye. Partial coherence occurs when two waveforms have almost the same frequency. In the eye, the wavelengths employed are such that an interference pattern occurs every few meters. This inference pattern is detected electronically. If one of the beams takes a detour, then the position of the interference pattern moves. By adjusting the light path of the other beam by a measureable distance to restore the interference pattern to its original site, the duration of the first beam’s detour can be measured.
Imagine that two partially coherent light beams are shone into the eye: One beam travels to the back of the eye, and the other reflects off the front of the cornea. They are now no longer causing an interference pattern on the detector. However, one beam reflects off the two mirrors in the machine, and they can be adjusted so that the time taken for the detour in the eye is the same as that taken between the mirrors. When this state is reached, the interference pattern is again visible at the detector. At that exact point, the time taken by the beam to travel between the mirrors is the same as the time taken for the other beam to travel the length of the eye (Figure 2). (In quantum physics, it is the same photon that travels each path at the same time.)
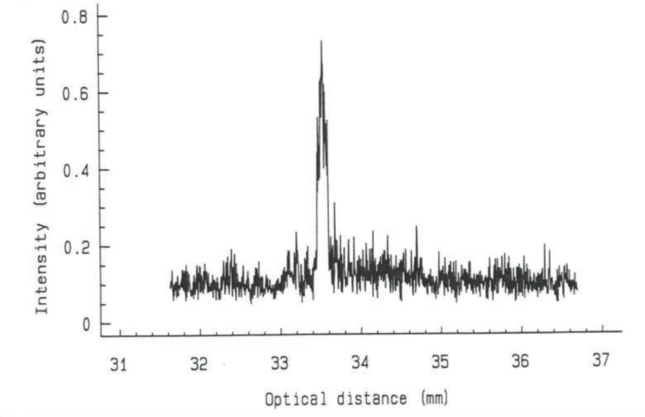
Figure 3. The larger gap between the mirrors (34 mm) is because the light slows in the eye and takes longer to traverse it.
However, the speed of light is slower in the eye than in the air. As a result, the distance between the mirrors is geometrically greater than the axial length of the eye being measured (Figure 3). Therefore, the machine must be calibrated to read the distance, not time of the detour. This has been achieved by measuring eyes with both optical and immersion biometry techniques and constructing a table so that partial coherence interferometry can give a reading in geometric distance rather than optical distance. Optical biometry has earned the reputation of being highly accurate in measuring axial length. This largely comes from the fact that it is independent of the operator and will not measure difficult eyes.

Estimating effective lens position
The final guess in the biometry process is regarding where the IOL will sit in the eye. As stated previously, any anteroposterior shift away from where the IOL is predicted to be will lead to significant refractive effect. As with the other measurements, there is no way to accurately measure where the IOL will sit in the eye postoperatively. Many investigators have attempted to use preoperative measurements not directly related to the postoperative IOL position to guess where it will lie. These measurements have included K readings (corneal height), preoperative ACD, and lens thickness, but all are no more than attempts to estimate where the IOL will position itself postoperatively. There is increasing interest in examining the anatomy of the ciliary body preoperatively to see if there are data that can be used to predict the IOL position.
CONCLUSION
Clearly, current biometry technology has been pushed to its limit. No amount of tweaking of formulas or K readings or axial length or ray tracing will overcome the fact that current technology forces surgeons to make too many guesses about data we cannot measure accurately enough in each individual patient. I believe that no further improvement in biometry is possible with our current methods. However, only a breakthrough in new technology will deliver this paradigm shift.


