
In the modern era of cataract surgery, where patient expectations are increasingly high, accurate and reliable IOL power selection is crucial. For many years now, surgeons have relied on incremental improvements to theoretical formulas. And while preoperative planning continues to significantly improve, outcomes have not always been consistent.
A fundamental problem with any theoretical formula is that the effective lens position—representing a significant portion of the calculation—is something that can only be estimated and not directly calculated. Recent improvements, like the Barrett Universal II and the Olsen formulas, do an outstanding job in this area, but, at the end of the day, the effective lens position remains a sophisticated estimation.
It is also an unfortunate reality that many surgeons and their staffs are still using older third-generation, two-variable formulas. I am quite certain that these same physicians no longer drive a car from 1988, have a TV from 1991, or use a cell phone from 1993, yet they continue to use IOL power selection methods from these years. Given the fact that we, as surgeons, are now being judged by our patients, and by our peers, by our refractive outcomes, the time has arrived to move to calculation methods from this century.
For the past 6 years, I have been working with the engineers and mathematicians at MathWorks (a world leader in mathematical modeling), Haag-Streit, and a large group of dedicated surgeoninvestigators to develop a new method of IOL power selection using pattern recognition. Based in artificial intelligence, the Hill Radial Basis Function (Hill-RBF) method (Figure 1) is entirely data driven and seemingly free of calculation bias. It also does not depend on the effective lens position.

Figure 1. A screen shot of the Hill-RBF calculator and explanation of its functions.
HOW DOES THIS WORK?
A radial basis function (RBF) neural network is a form of sophisticated mathematical modeling.1 Although it may sound unfamiliar, or even exotic, its use in the modern world is all around us. EKG interpretation, fingerprint identification, facial recognition, sophisticated financial forecasting, and engine calibration and operation are just a few commonly applied applications that many of us may already have used without being aware.
The fundamental advantage of pattern recognition for selecting IOL power is achieved through the process of adaptive learning—the ability to learn tasks based solely on data and independent of what is previously known. Theoretical formulas limit possibilities to situations that are already understood. This method is also self-organizing, meaning that it has the ability to create an independent representation of data. Such an approach is well suited to the complex, nonlinear relationships that make up many aspects of the human eye.
For example, for an axial length of 23.5 mm, consider how many associated combinations of keratometry (K), anterior chamber depth (ACD), lens thickness, and white-to-white are possible; it is therefore easy to imagine why theoretical, regression-based formulas may perform below expectations in certain situations. Most surgeons have a preferred method for short or long eye, steep or flat Ks, and unusual combinations. For the RBF method, combinations of preoperative measurements are instead viewed as a pattern. And when this is combined with a sophisticated form of data interpolation, it becomes free of calculation bias.
The use of RBFs for IOL power selection fundamentally is a big data exercise. The greater the number of individual cases that are fit to the RBF model, the better it will perform. When creating the Hill-RBF method, we started out with data from about 680 Lenstar (Haag-Streit) measurements. In its present form, it is now based on 3,445 eyes measured by the Lenstar. By the end of 2016, an additional 1,400 short eyes, along with 9,000 normal and long eyes, will be used to update the existing Hill-RBF model.
With increasing data, the breath and depth of the RBF model is expanded, improving both the accuracy of pattern recognition and data interpolation. Stated differently, the more cases we have, the smarter the RBF method becomes. This is enormously powerful technology limited only by the amount and the quality of the data used to augment it.
SELF-VALIDATION
Another component of the RBF method is the concept of selfvalidation. This is achieved through the use of multiple, pair-wise boundary models, such as ACD versus axial length (Figure 2).
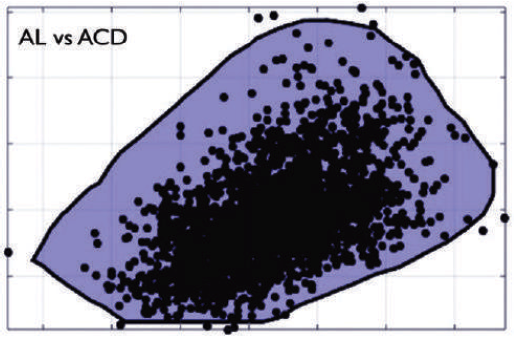
Figure 2. Axial length versus anterior chamber depth, one of six pair-wise boundary models for the RBF method. If a preoperative measurement falls outside the blue area, the calculation will be flagged with an out-of-bounds indication.
A boundary model is a commonly used engineering tool to aid in accuracy prediction for individual calculations. For IOL power selection, when all preoperative measurements reside within each of six pair-wise boundary models, the IOL power recommendation is deemed as being an in-bounds calculation (Figure 3), and the likelihood that the intended outcome will be achieved is high. When any preoperative measurement resides outside one of the pair-wise boundary models, the IOL power recommended is flagged as being an out-of-bounds calculation (Figure 4). An out-of-bounds indication tells the user that the intended outcome may not necessarily be achieved.
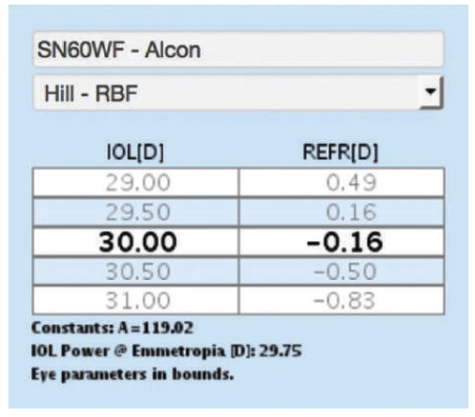
Figure 3. Close-up screen shot of an IOL power calculation with an in-bounds calculation.
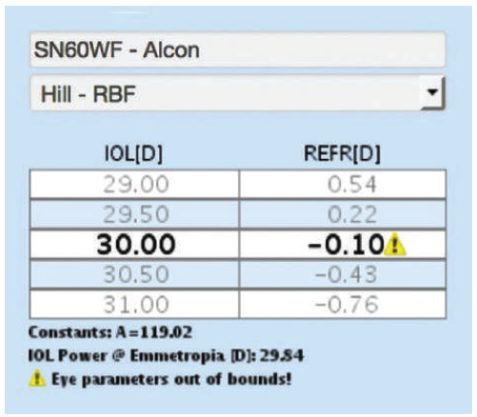
Figure 4. Close-up screen shot of an IOL power calculation with an out-of-bounds calculation.
While there will always be exceptions, with the RBF method, an in-bounds indication when the eye has been measured by the Lenstar typically has an accuracy of ±0.50 D of approximately 90%. Lenstar users typically cross reference this with the Barrett Universal II and Olsen formulas.
PROSPECTIVE TESTING
In order to evaluate the usefulness of the Hill-RBF method in clinical practice, Michael E. Snyder, MD; Stephen Scoper, MD; and I conducted a prospective study of 459 consecutive surgeries with a beta version of the Hill-RBF calculator. Using the typical benchmark for intended correction of ±0.50 D, we found that, with the Hill-RBF calculator, 91% of all eyes with an in-bounds indication were within this range. Furthermore, 92% of normal eyes, 98% of eyes with high axial myopia, and 84% of eyes with high axial hyperopia—eyes that are more prone to end up with a refractive surprise—were within ±0.50 D of the target spherical equivalent postoperatively. This result is certainly as good as and, quite possibly, even better than any other methodology currently available.
Wang and others conducted a study of 86 eyes and concluded that the Hill-RBF method had the best overall accuracy for eyes with high axial hyperopia (axial length < 22 mm) than any other IOL power formula they used.2 Furthermore, both our prospective study and the study presented at ARVO2 used an RBF model that had only been fit to 3,445 eyes. As more cases are added to the RBF model-fitting dataset, it is likely that the accuracy for these unusual eyes will continue to improve.
I have been using the Hill-RBF calculator in my practice since September 2015. Although I continue to crosscheck the results from the Hill-RBF method with the Barrett Universal II and the Olsen formulas, the recommendations are remarkably similar. At the present time, the Hill-RBF method, at the very least, is on par with the best theoretical formulas. It is the goal of all who are involved in this project that in the near future we are going to be even better.
WE CAN ALL DO BETTER
For more than a decade, I have offered my services, free of charge, to optimize physicians’ databases. So far, I have about 260,000 cases in which to draw from.
Using that data, it appears that less than 1% of physicians achieve postoperative refractive outcomes that are within ±0.50 D of intended correction in at least 92% of cases. About 6% of physicians are within this range in about 84% of cases, and the other 93% are within this range about 78% of the time. (It is important to note that these statistics were calculated after the removal of outliers and after the optimization of lens constants.)
As we all know, patient expectations today are high, especially in those selecting premium IOLs such as multifocal and toric lenses. The bottom line is that we can all be doing better, and I believe that the Hill-RBF method can be one way to achieve consistently better refractive outcomes.
GROWING THE DATABASE
There are currently 25 beta test sites in 14 countries from which we continue to collect Lenstar biometry data and surgical outcomes. In a further attempt to grow the database, a website was launched the first week in May 2016, www.rbfcalculator.com. This open-access site allows surgeons to use this method to select an IOL power for their patients. If a user email address is entered, 3 months later, they will receive an email asking for the make, model, and power of the IOL implanted and also the patient’s final refractive outcome. And while the Hill-RBF method was optimized for the Lenstar, it can still be used with other biometers. Ideally, biometers other than the Lenstar should employ high-density keratometry and all axial measurements should be by optical biometry.
In the past 5 months, our beta testers have provided more than 10,000 Lenstar cases. Imagine where this project will be 5 years from now, with the potential for 100,000 or even 200,000 cases. This is exciting to consider.
HOW TO USE
Instructions for use of the Hill-RBF calculator can be found at http://rbfcalculator.com/docs/Hill-RBF-Calculator-Instructions.pdf.
Although The Hill-RBF method will only available on the Lenstar for the foreseeable future, anyone can use the calculator on the website by simply selecting the appropriate biometry method from the drop-down menu.
What makes this project unique is that it has taken the form of a worldwide collaborative effort. All users of the online calculator will have the option to participate in future revisions. In this way, everybody has a stake in its success. In the last 17 weeks there have been over 35,700 calculations. It is wonderful to see the ophthalmic community so readily accepting of this new technology.
1. Bors AG. Introduction of the Radial Basis Function (RBF) Networks. Accessed October 19, 2016.
2. Wang L, Gokce S, Zeiter, Weikert MP, Hll WE, Koch DD. Comparison of seven IOL power calculation formulas in eyes with axial length ≤ 22 mm. Poster presented at ARVO; May 1-5, 2016; Seattle.

